Interpreting Correlation in Multi-Test Analysis

Correlation is a statistical relationship calculated to describe linear data between two variables. While correlation does not guarantee a meaningful relationship between two data sets, it implies that a relationship might require further investigation and discovery. 

Interpreting Meaningful Correlation

Multi-Test Analysis uses the Pearson correlation coefficient to describe the linear shape between two assessment data sets. The system calculates the correlation using the raw score for both assessments or, if applicable, the RIT score. The goal is to determine if there is a potential relationship between the scores of one assessment and the scores of another. An example practice is to decide if local assessments are predictive of a summative assessment, such as whether local tests predict performance on the end-of-year exam. 

To help decide if the correlation coefficient is meaningful, we also provide an Achievement Level Comparison chart so users can see how students may have changed from one performance band into another. Reviewing this data helps local users decide if the relationship between the two data sets is meaningful in determining if students are progressing.

Below are a few examples of how correlation can imply a relationship between two data sets.

Perfect Correlation

In a Perfect Correlation example, the two assessment data sets imply a perfect linear relationship. All data points fall on a line, which may indicate that student performance on one assessment predicts the performance on another.

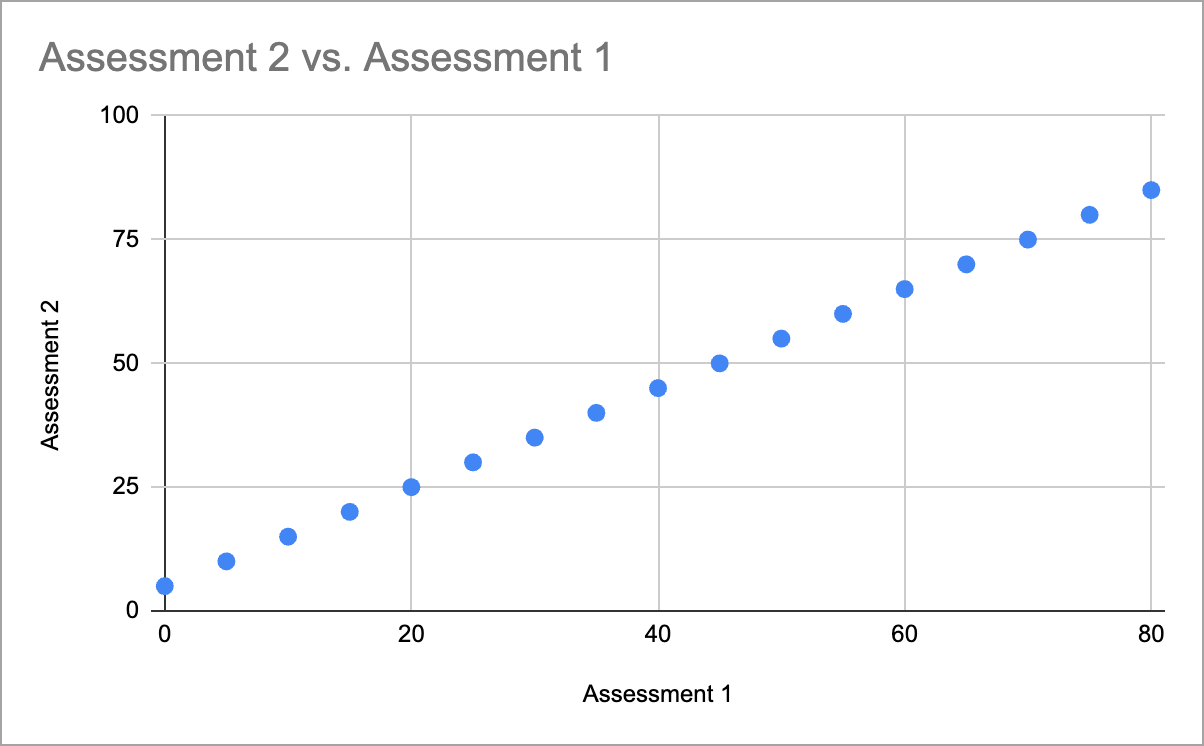
Perfect Correlation graph (correlation coefficient = 1.0)

Perfect Negative Correlation

In a Perfect Negative Correlation example, the two assessment data sets imply a perfect negative linear relationship. All data points fall on a line but indicate that the performance on one assessment inversely predicts performance on the other for all students.

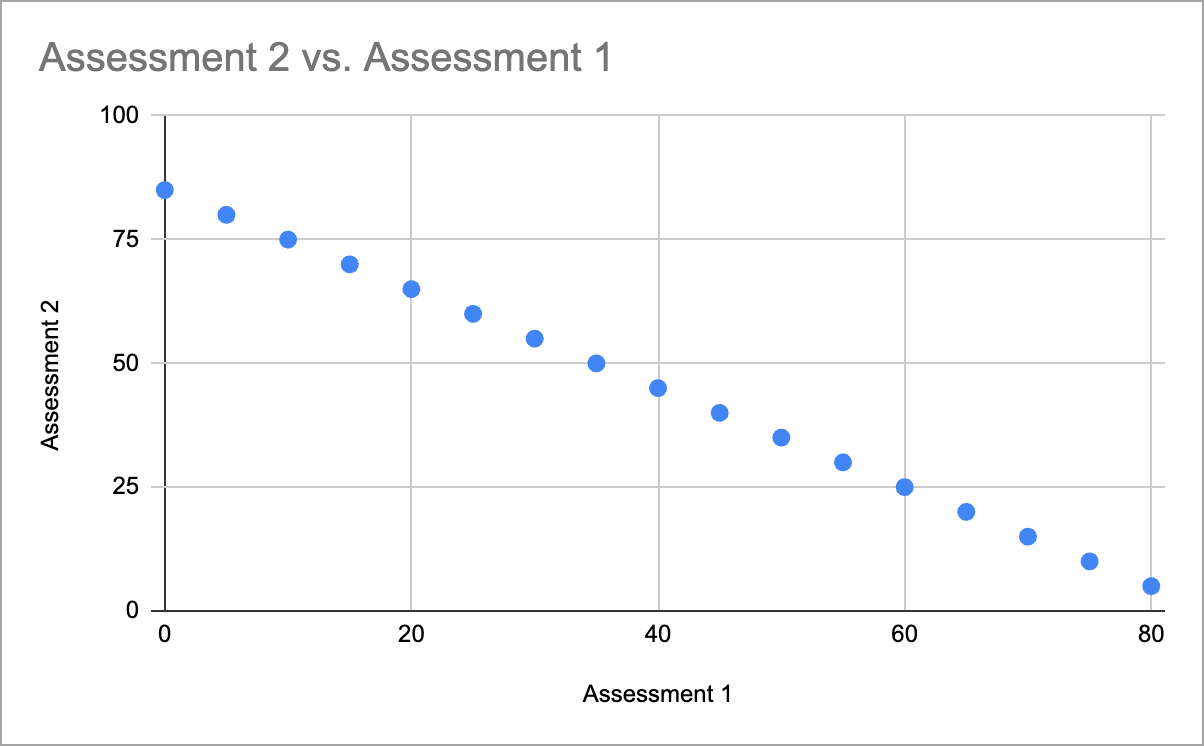
Perfect Negative Correlation graph (correlation coefficient = -1.0)

No Relevant Correlation

In a No Relevant Correlation example, the two data sets imply no significant linear relationship. You cannot make a line to approximate the performance between the two assessments. One assessment cannot predict the performance of another.

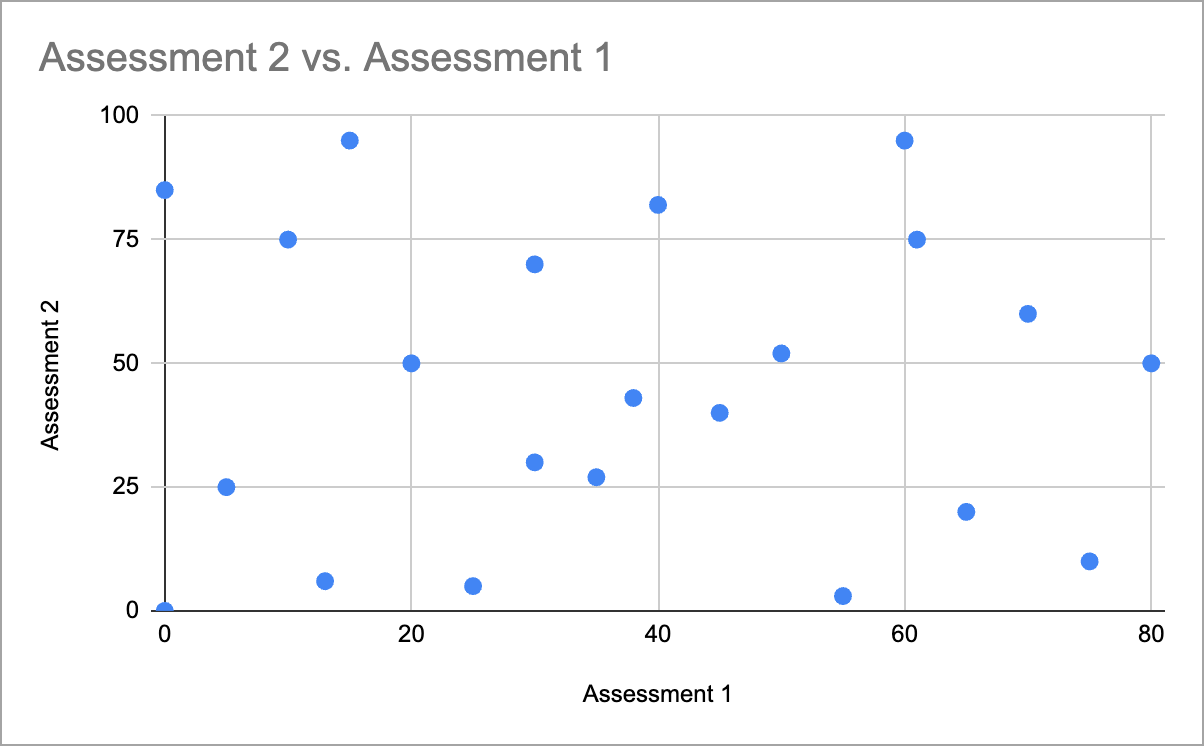
No Relevant Correlation graph (correlation coefficient = 0)

A Significant Correlation

In most accepted research, a significant correlation would be greater than 0.5, with increasing confidence the closer the value gets to 1.0. However, correlation values are not enough in isolation. There are some scenarios where there could be a strong correlation, but accurately predicting student performance is not guaranteed. 

In the example below, the correlation is a strong 0.89. That value alone might indicate that one assessment accurately predicts the performance of the other. However, the data points reveal a marked improvement in student performance from assessment 1 to assessment 2, where most students improved their performance by double digits. This improvement may or may not be a desired fluctuation in student performance. 

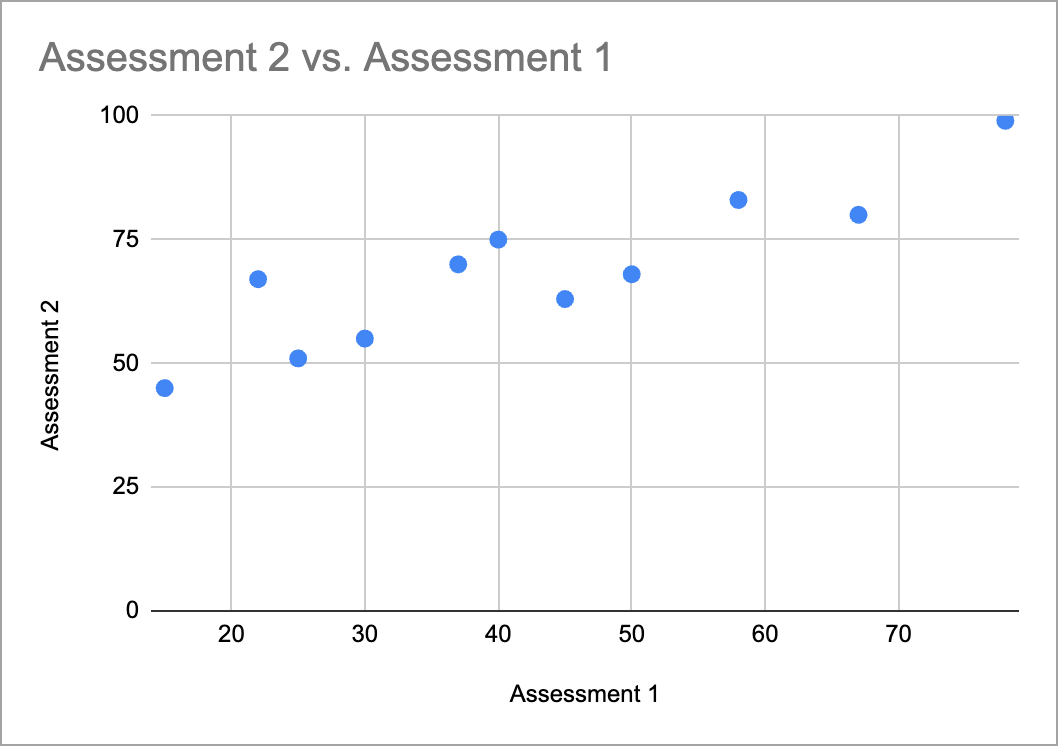
Significant Correlation graph

In some scenarios, a district may decide this is an accurate prediction. Perhaps an intervention is proving to be effective and increasing student scores. In other scenarios, a district may decide this is not an accurate prediction and decide to dig deeper into one assessment to determine if it was too easy or if one was too difficult.

The Correlation View in Multi-Test Analysis

To supplement the correlation value, the Correlation View in Multi-Test Analysis includes an Achievement Level Comparison. The Achievement Level Comparison allows users to see how many Achievement Levels students moved between test 1 and test 2. 

In many instances, if students did not move Achievement Levels or moved very few, then the data is likely very consistent. Consistent data with strong correlation scores provides even greater confidence that one test is predictive of another. 

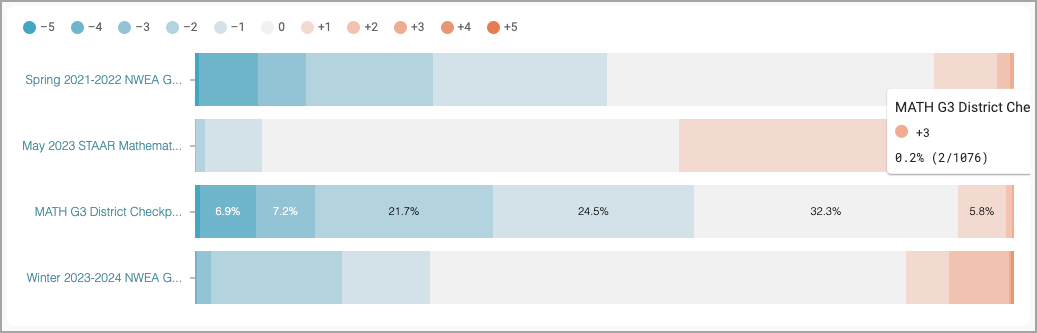
For the third assessment, Math G3 District Checkpoint, most students (60.3%) dropped one or more Achievement Levels in the Graph view. 

When looking at the data in the Table view, you can see the actual number of students for each Achievement Level comparison. These numbers may indicate that a user needs to analyze the assessment for difficulty. 

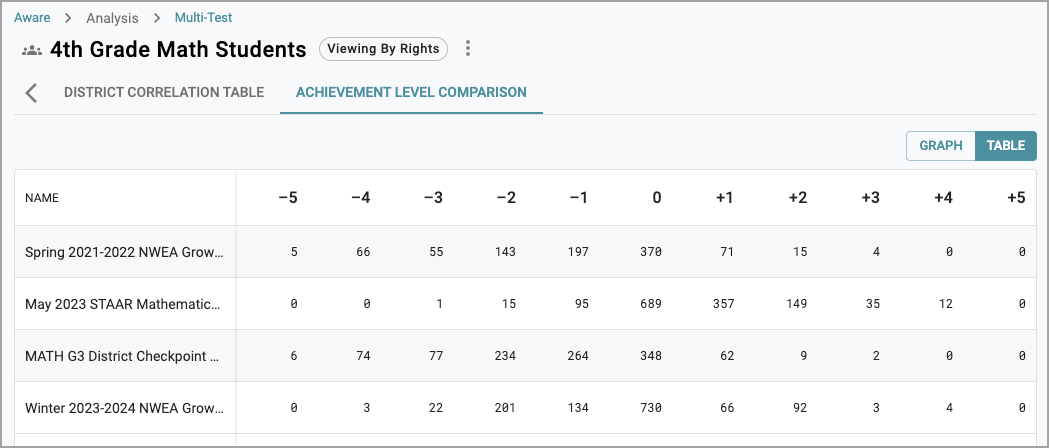
Conversely, the May 2023 STAAR Mathematics test shows that a considerable portion of students didn’t change Achievement Levels or only rose by one Achievement Level. This may imply performance stability and a high level of predictiveness from one assessment to the other.

Looking at the assessment in Single Test Analysis may prove helpful in deciding why student performance shifted so much. Knowing this can help users determine if the correlation score truly does imply a performance relationship between the two assessments.